Алгоритм Франка

Дмитрий Урбанович

Ижевск, 15—16 июня 2018

Обновлено 9 января 2021 (MathML)

Алгоритм Франка — это легкий по затратам памяти алгоритм, который моделирует один запуск квантового компьютера. Выдается одно базисное состояние, случайно выбранное из распределения, соответствующего заданной квантовой цепи и начальному состоянию.

Пусть нам дано $t$ унитарных преобразований $U_1$, $U_2$, ..., $U_t$ и начальное состояние $t$ кубитов в виде вектора ${\psi }_0$ размерности $2^n$. Тогда определим состояние кубитов после применения $U_i$ рекуррентно: $${\psi }_i=U_i\cdot {\psi }_{i-1}$$

Первый способ промоделировать поведение квантового компьютера заключается в том, чтобы использовать генератор псевдослучайных чисел по распределению ${\psi }_t\circ {\psi }_t^{\ast }$ (покомпонентное произведение вектора с его комплексным сопряжением). Недостаток способа в том, что вектор ${\psi }_t$ имеет $2^n$ компонентов: для $n=40$ получится ${10}^{12}$ чисел, которые вряд ли влезут в оперативную память вашего компьютера.

К счастью, существует теорема $\mathrm{BQP}\subseteq \mathrm{PSPACE}$. Ее доказательство заключается в том, чтобы вычислять одну компоненту вектора ${\psi }_{t,k}$ рекурсивно и без сохранения промежуточных результатов. $${\psi }_{t,k}=\sum _{i=0}^{2^n-1}{U}_{t,k,i}\cdot {\psi }_{t-1,k}$$ В реальности большинство из слагаемых этой суммы равны нулю. Например, для Тоффоли, $\mathrm{cNOT}$ и других «классических» вентилей количество ненулевых слагаемых равно одному, а для вентиля Адамара — двум. Таким образом, каждый компонент ${\psi }_t$ вычисляется за $O\left(2^t\right)$.

Такой подход экономит память, но требует перебирать много конечных состояний: в квантовой механике трудно предсказать, какие из них будут иметь вероятности около нуля.

Майкл Франк в 2009 году воспользовался идеей Дэвида Бома: квантовая система находится в одном определенном базисном состоянии в каждый момент времени. Если очередное преобразование относится к классическим вентилям, то просто выполняется детерминированный переход. Если же это, к примеру, вентиль Адамара, то делается случайный выбор из двух возможных состояний $k_1$ и $k_2$. Первое состояние будет выбрано с такой вероятностью: $$p_{i,k_1}=\frac{{\left|{\psi }_{i,k_1}\right|}^2}{{\left|{\psi }_{i,k_1}\right|}^2+{\left|{\psi }_{i,k_2}\right|}^2}$$

Алгоритм выполняет всю квантовую цепь за $O\left(2^t\right)$, так как верно следующее равенство: $$\sum _{i=0}^{t-1}{2}^i=2^t-1$$

Алгоритм выдает конечные состояния в соответствии с распределением ${\psi }_t\circ {\psi }_t^{\ast }$. Это доказывается по индукции: предположим, что на шаге $t-1$ любое состояние $k_i$ выбирается с корректной вероятностью ${\left|{\psi }_{t-1,k_i}\right|}^2$. Тогда:

1. Если $U_t$ — «классический вентиль», то новое состояние будет выбранно также с корректной вероятностью. Это следует из того, что такие преобразования всего лишь делают перестановку амплитуд.
2. Если $U_t$ — вентиль Адамара, то все состояния делятся на пары $k_1$ и $k_2$ для преобразования. Заметим, что для любой такой пары верно равенство: $${\left|{\psi }_{t-1,k_1}\right|}^2+{\left|{\psi }_{t-1,k_2}\right|}^2={\left|{\psi }_{t,k_1}\right|}^2+{\left|{\psi }_{t,k_2}\right|}^2$$ Тогда $k_1$ будет выбран при переходе либо из $k_1$, либо из $k_2$ с такой вероятностью: $${\left|{\psi }_{t-1,k_1}\right|}^2\cdot p_{t,k_1}+{\left|{\psi }_{t-1,k_2}\right|}^2\cdot p_{t,k_1}={\left|{\psi }_{t,k_1}\right|}^2\cdot \frac{{\left|{\psi }_{t-1,k_1}\right|}^2+{\left|{\psi }_{t-1,k_2}\right|}^2}{{\left|{\psi }_{t,k_1}\right|}^2+{\left|{\psi }_{t,k_2}\right|}^2}={\left|{\psi }_{t,k_1}\right|}^2$$

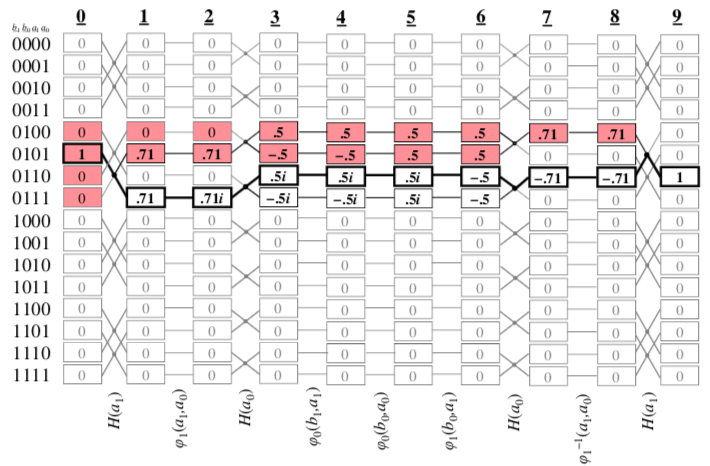
Напоследок приведем иллюстрацию из оригинальной статьи, которая показывает преимущества алгоритма для целей отладки.